Mahkûmun İkilemi

Puccini’nin Tosca adlı operasında, kadın kahraman berbat bir ikilem içinde kalır. Kadının aşığı Cavaradossi, polis şefi Scarpia tarafından ölüme mahkûm edilmiştir, fakat Scarpia Tosca’ya bir öneri getirir. Eğer Tosca kendisiyle yatarsa, polis şefi, idam mangasına kurusıkı kullanmaları talimatını vererek Cavaradossi’nin hayatını bağışlayacaktır. Tosca, Scarpia’nın önerisini kabul eder fakat polis şefinin mangaya kurusıkı kullanması yönünde talimat vermesinin ardından, onu bıçaklar. Polis şefini öldüren Tosca, Scarpia’nın da kendisini kandırdığını çok geç de olsa fark eder. İdam mangası gerçek mermi kullanmıştır; Cavaradossi yaşamını yitirir. Tosca intihar eder; ve sonuçta her üçü de ölüp gider.

Tosca ve Scarpia, böyle adlandırmamış olsalar da, aslında bir oyun oynuyorlardı. Bu oyun, matematiğin biyoloji ile ekonomi arasında köprü kuran, ezoterik bir dalı olan oyun kuramı içerisinde en bilinen oyundur. Oyun, son yılların en heyecan verici bilimsel keşiflerinden birinin de ana temasıdır: Bu keşif insanların birbirlerine neden iyi davrandıklarına yönelik kavrayıştan başka birşey değildir. Üstelik, gerek Tosca gerekse de Scarpia, her ikisi için de felaketle sonuçlanmasına rağmen bu oyunu, tam da oyun teorisinin öngördüğü biçimde oynamışlardır. Bu nasıl olabilir?

Bilgisayarlar işbirliği yapmayı öğrenirler

Bu oyun mahkûmun ikilemi olarak bilinmektedir ve her nerede çoğunluğun iyiliği ile kişisel çıkar arasında bir çatışma varsa orada geçerlidir. Eğer yaptıkları pazarlığa sadık kalmış olsalardı. hem Tosca hem de Scarpia kazançlı çıkacaklardı: Tosca aşığının hayatını kurtaracak, Scarpia da onu yatağa atmış olacaktı. Fakat, Tosca ya da Scarpia, karşısındakinin pazarlığa sadık kalmasını sağlayıp, kendisi döneklik yapmış olsaydı, birey olarak her biri, kendi adına daha da büyük bir çıkar sağlamış olacaktı: Tosca hem aşığını kurtarmış hem de iffetini korumuş olacak, öte yandan Scarpia ise hem Tosca ile yatmış ve hem de düşmanından kurtulmuş olacaktı.

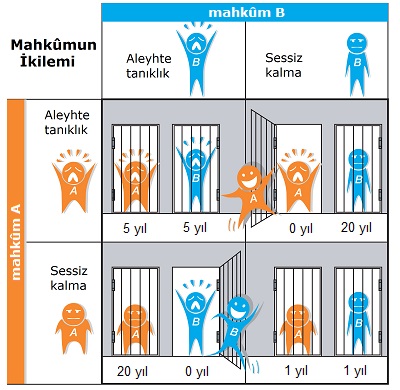
Mahkûmun ikilemi, benciller arasında nasıl işbirliği sağlanacağına dair bizlere yalın bir örnek sunar – yasaklar, manevi kısıtlamalar ya da ahlaki zorunluluğa bağlı olmayan işbirliği. Nasıl olur da bireyler, kişisel çıkarlarınca yönlendirilip çoğunluğun yararına hizmet ederler? Bu oyun mahkûmun ikilemi diye adlandırılır çünkü, oyunu açıklayan anektodlar arasında en bilineni, kendi aldıkları cezada indirim yaptırtmak amacıyla birbirleri aleyhine tanıklık edip, kanıt sunma seçeneği olan iki mahkûma dair olanıdır. Ortaya bir ikilem çıkar çünkü eğer mahkûmlardan biri de öteki de, diğeri aleyhine tanıklık etmez ise, polis her ikisini de daha az bir cezaya çarptırıp, mahkûm edebilir; böylece sessiz kaldıkları takdirde, her ikisi de karlı çıkar; fakat karşısındaki sessiz kalmasına karşın, onun aleyhine tanıklık eden mahkûm, birey olarak daha büyük çıkar sağlar.

Neden? Mahkûmları boşverin ve bunu, puan elde etmek için başka bir oyuncuyla oynadığınız bir oyun olarak düşününün. Eğer her ikiniz de işbirliği yaparsanız (sessiz kalırsanız) her biriniz üç puan elde edersiniz (buna “ödül” diyelim); eğer her ikiniz de birbiriniz aleyhine tanıklık ederseniz birer puan alırsınız (buna da “ceza” diyelim). Fakat biri aleyhte davrandığı, diğer oyuncu ise işbirliği yaptığı takdirde, işbirliği yapan hiç puan almaz (“enayinin ödediği diyet”); ve döneklik yapan ise beş puan alır (“cazibe”), Dolayısıyla eğer karşınızdaki oyuncu döneklik yaparsa, sizin de döneklik yapmanız çıkarınıza olacaktır. Bu durumda hiç olmazsa bir puan elde edersiniz. Fakat eğer karşınızdaki işbirliği yaparsa, siz döneklik yaparak daha da büyük bir çıkar sağlarsınız: üç puan yerine beş puan elde edersiniz. Karşınızdaki ne yaparsa yapsın, siz döneklik yaparak daha büyük bir çıkar elde edersiniz. Ama aynı sav, karşınızdaki için de geçerli olduğundan, karşılıklı döneklik kesin akıbettir: Üçer puan alabilecekken, her biriniz birer puan alırsınız.

Erdemliliğiniz sizi yanıltmasın. Her ikinizin de işbirliği yaparak asilce bir davranışta bulunduğunuz gerçeğinin konuyla hiçbir ilgisi yoktur. Bizim aradığımız, yapılması “en doğru olan şey değil, manevi bir “vakuum” içerisinde, mantığa “en uygun” davranıştır. Ve bu da döneklik yapmaktır. Bencil olmak akılcıdır.

Geniş tanımıyla, mahkûmun ikilemi son derece eskiye dayanan bir kavramdır. Kuşkusuz Hobbes bunu anlamıştı. Kısa, fakat çok bilinen ‘geyik avı’ hikayesinde, bunun koordinasyon oyunu olarak bilinen bir uyarlamasını tesadüfen epey detaylı bir biçimde tanımlayan Rousseau da bunu kavramıştı. Ava çıkmış bir grup ilkel erkeği betimleyen Rousseau, şöyle aktarır:

Rousseau’nun ne kastettiğini açıklayacak olursak; farz edin ki kabiledeki herkes geyik avlamaya çıkar. Avcılar geyiğin yattığı çalılıkların etrafında geniş bir çember oluştururlar ve sonunda hayvan, etrafındaki bu kordondan kaçmak zorunda kalana dek avcılar ilerleyerek çemberi daraltırlar, ki bu noktada, eğer her şey yolunda giderse, geyiğe en yakın avcı hayvanı vurup öldürür. Fakat diyelim ki, avcılardan biri bir tavşanla karşılaşır. Kuşkusuz bu avcı tavşanı yakalayabilir fakat bunu ancak çemberden ayrılarak yapabilir. Böylelikle çemberde bir boşluk meydana gelir ve geyik de bu boşluktan kaçıp gider. Tavşanı yakalayan avcı istediği eti elde ederek tatmin olmuştur fakat diğerleri onun bencilliğinin bedelini boş bir mideyle öderler. Birey için doğru olan karar, grup için yanlıştır ki bu da sosyal işbirliğinin ne denli umutsuz bir proje olduğunu kanıtlar (demiştir, insanlara itimat etmeyen Rousseau sevimsiz bir ifadeyle).

Geyik avının, Douglas Hofstadter tarafından ortaya atılan ve “kurdun ikilemi” denen modern bir uyarlaması vardır. Yirmi kişi, parmakları düğmelerin üzerinde, birer kabinin içerisinde oturmaktadırlar. Aradan on dakika geçtikten sonra, hiç kimse düğmeye basmadığı takdirde herkes biner dolar kazanacaktır; biri düğmeye bastığı takdirde, düğmeye basan yüz dolar kazanacak, diğerleri ise hiçbir şey alamayacaktır. Eğer akıllıysanız, düğmeye basmayıp bin doları alırsınız; fakat eğer çok akıllıysanız, küçük bir ihtimal de olsa birinin düğmesine basabilecek kadar aptal olabileceğini görürsünüz ki bu durumda herkesten önce kendi düğmenize basarsanız daha karlı çıkarsınız; ve şayet çok çok akıllıysanız, çok akıllı insanların bu sonuca varacağı ve düğmelerine basacaklarını kavrayıp, iyisi mi siz de kendi düğmenize basarsınız. Mahkûmun ikileminde olduğu gibi, doğru mantık sizi kolektif bir felakete sürükler.

Eski bir fikir olsa da, mahkûmun ikilemi ilk olarak 1950’lerde, California’daki RAND kuruluşundan Merril Flood ve Melvin Drescher tarafından bir oyun olarak biçimlendirildi ve birkaç ay sonra, Princeton Üniversitesi’nden Albert Tucker tarafından ilk defa mahkûmlara dair bir anektod olarak farklı bir biçimde ifade edildi. Flood ve Drescher’in farkına vardığı üzere, mahkûm ikilemleri her yerde karşımıza çıkmaktadır. Kabaca ifade edilecek olursa, yapmak için dayanılmaz bir istek duyduğunuz, fakat herkes aynı şeyi yaparsa bunun büyük bir hata olacağını bildiğiniz herhangi bir durum bir mahkûmun ikilemi durumu olabilir (Mahkûmun ikileminin formel matematiksel tanımı, cazibenin ödülden, ödülün cezadan, cezanın da enayinin ödediği diyetten daha büyük olduğu herhangi bir durumdur fakat çok büyük bir cazibe söz konusuysa, oyun değişir.) Eğer kimsenin araba çalmayacağına güvenilebilseydi, arabaların kapılarının kilitlenmesine gerek duyulmazdı ve sigorta primleri, güvenlik aygıtları ve benzeri konularda zaman ve maliyetten büyük miktarda tasarruf edilirdi. Bu herkesin çıkarına olurdu. Fakat böylesine güvenilir bir dünyada, bir birey toplumsal sözleşmeden cayıp, bir araba çalarak daha da büyük bir çıkar sağlardı. Aynı şekilde, şayet herkes avlanma konusunda getirilen kısıtlamalara uyarak çok fazla balık avlamasaydı, bu tüm balıkçıların çıkarına olurdu; fakat herkes avlayabildiği kadar balık avlıyorsa, avlanma kısıtlamasına uyan balıkçı sadece kendi payını daha bencil bir balıkçıya kaptırmış olur. Dolayısıyla, bireyselliğin kolektif bedeline hepimiz katlanırız.

Garip ama, tropik yağmur ormanları, mahkûm ikilemlerinin ürünleridir. Bu ormanlarda yetişen ağaçlar, enerjilerinin büyük bir kısmını, üremekten çok gökyüzüne doğru uzamak için harcarlar. Şayet bu ağaçlar, rakipleriyle bir anlaşmaya varıp, büyük tomrukları yasadışı ilan ederek, ağaç boyunda üç metrelik bir sınırlamaya uysalardı, bu her ağaç için daha iyi olurdu. Fakat bunu yapamazlar.

Yaşamın karmaşıklığını aptalca bir oyuna indirgemek, ekonomistlerin adını kötüye çıkaran bir şeydir. Fakat mesele gerçek hayatta karşılaşılan her sorunu “mahkûmun ikilemi” adında bir kutunun içine sıkıştırmaya çalışmak değil, kolektif ve bireysel çıkarlar çatıştığında neler olacağına dair ideal bir uyarlama/model ortaya koymaktır. O zaman, ideal olanla deney yapabilirsiniz, ta ki şaşırtıcı bir keşif yapana dek; sonra gerçek dünyaya dönerek bunun gerçek olaylara ışık tutup tutmayacağını görebilirsiniz.

Mahkûmun ikilemi oyunuyla ilgili olan tam da budur (bazı kuramcıları, çeke çeke, zorla gerçek dünyaya döndürmek zorunda kalınmasına rağmen). 1960’larda, matematikçiler, mahkûmun ikileminden çıkarılan tatsız dersten –dönekliğin/caymanın tek akılcı yaklaşım olduğu sonucundan- kaçınmak için neredeyse çılgıncasına bir arayış içerisine girdiler ve defalarca, buna bir çözüm getirdiklerini ileri sürdüler. Bunların arasında en dikkat çekici olanı, 1966 yılında Nigel Howard’ın, oyunu, oyuncuların eylemlerinden ziyade niyetlerine göre yeniden ve farklı biçimde ifade ettiği çözüm önerisiydi. Fakat, önerilen diğer tüm çözümler gibi, Howard’ın bu paradoksa yönelik çözümünün de sadece hüsnü kuruntudan ibaret olduğu görüldü. Önerilen oyunun başlangıç koşullarına göre, işbirliği mantıksız bir şeydir.

Bu çıkarım salt ahlaka aykırı olduğundan değil, gerçek insanların davranış biçimleriyle büyük ölçüde çelişkili olduğundan asla benimsenmedi. İşbirliği, insan topluluklarının değişmez bir unsuru olmuştur; sosyal ve ekonomik yaşamın temeli tam da bu güven kavramıdır. Sizce bu mantık dışı mıdır? Birbirimize karşı iyi ve şefkatli olmak için içgüdülerimizi bastırmak mı zorundayız? Suç işlemenin kimseye faydası var mı? İnsanlar salt çıkar sağlamak için mi dürüst davranırlar?

1970’lerin sonuna gelindiğinde, mahkûmun ikilemi, ekonomistlerin bireysel çıkar saplantılarına dair yanlış olan her şeyi simgeliyordu. Şayet oyun, böyle bir ikilem karşısında bireyin bencil davranmasının akılcı bir eylem olduğunu ispatladıysa, o zaman bu yalnızca varsayımın yetersizliğini ispatlamıştır. İnsanlar değişmez bir biçimde bencil olmadıklarından, bireysel çıkardan değil toplumun iyiliğinden ötürü motive olurlar. Dolayısıyla, bireysel çıkar üzerine inşa edilmiş iki yüz yıllık klasik ekonomi, çözümü yanlış yerde arıyordu.

Oyun kuramı üzerine konu dışı bir saptama: 1944 yılında, büyük Macar matematikçi Johnny von Neumann’ın üretken fakat insanlıktan nasibini almamış beyninde filizlenen oyun kuramı, özellikle “kötümser bilim” ekonominin ihtiyaçlarına cevap veren bir matematik dalıdır. Bunun nedeni, oyun kuramının ilgi alanının, yapılacak doğru şeyin diğer insanların ne yaptığına bağlı olduğu bir dünyada yer almasıdır. İkiyle ikiyi toplamanın doğru yolu koşullara bağlı değildir, ama bir yatırım yapma ya da bir yatırımı elden çıkarma karan tümüyle koşullara ve özellikle de diğer insanların verecekleri kararlara bağlıdır. Gerçi bu durumda bile, hatasız davranmanın ve diğer insanlar ne yaparlarsa yapsınlar, işe yarar bir strateji gütmenin bir yolu olabilir. Buna ilişkin, yatırım kararı vermek gibi gerçek hayata uygun bir örnek bulmak, bir fark yaratmayacağı gibi muhtemelen imkansıza yakındır fakat bu, kusursuz stratejinin var olmadığı anlamına gelmez. Oyun kuramının ana fikri, kuramı, gerçek hayattaki durumların basitleştirilmiş uyarlamalarında bulmaktır – evrensel reçeteyi bulmak. Ticaret ve alım satım alanında bu, Princeton Üniversitesi’nden matematikçi John Nash’a atfen, ‘Nash Dengesi’ olarak anılmaya başlandı (John Nash, kuramı 1951. yılında ortaya koydu, ve uzun süren bir şizofreni hastalığını atlatmasıyla birlikte, 1994 yılında Nobel Ödülü aldı). Bir Nash dengesine göre, her bir oyuncunun stratejisi, diğer oyuncularca benimsenen stratejilere verilen en yerinde tepki olarak tanımlanır ve kimsenin seçtiği stratejiden sapma dürtüsü yoktur.

Örnek olarak, Peter Hammerstein ve Reinhar Selten tarafından icat edilen bir oyunu düşünün. Oyunda, Konrad ve Niko adında iki şahıs yer alır; bu ikisi, parayı birbirleriyle paylaşmak zorundadırlar. İlk oynayan Konrad parayı eşit olarak (adil) mi Yoksa oransız olarak (haksız) mı paylaşacağına karar vermelidir. Ardından oynayan Niko ise ne kadar parayı paylaşacaklarına karar vermelidir: Yüksek ya da düşük bir miktar. Şayet Konrad haksız oynarsa, Niko’nun alacağının dokuz katını kazanır. Şayet Niko yüksek oynarsa, her bir oyuncu, düşük bir paranın paylaşıldığı duruma kıyasla on kat daha fazla kazanır. Konrad, Niko’nun dokuz katı kadar para talep edebilir ve Niko’nun bu konuda yapabileceği hiçbir şey yoktur. Şayet Niko düşük oynarsa, hem kendini hem de Konrad’ı cezalandırmış olur. Dolayısıyla Niko’nun düşük oynayarak Konrad’a gözdağı vermesi bile akılcı değildir. Nash dengesine göre, Konrad haksız, Niko ise yüksek oynar. Niko açısından ideal sonuç olmasa da bu, kötünün iyisidir.

En iyi sonucun, mutlaka Nash dengesi ile elde edilmediğine dikkatinizi çekerim. Bilakis, genelde Nash dengesi oyunda yer alan eşlerden birini ya da her ikisini birden felakete sürükleyecek iki stratejiye bağlıdır ve bununla birlikte oyunculardan ne biri ne de öteki, alternatif stratejiyi benimseyerek daha iyi sonuç elde edemez. Mahkûmun ikilemi tam da böyle bir oyundur. Tecrübesiz iki oyuncuyla tek bir oyun oynandığında, tek bir Nash dengesi söz konusudur: Her iki oyuncu da döneklik yapar.

Şahinler ve Güvercinler

Sonra bir deney, bu sonucu tepetaklak etti. Bu deney, otuz yıl boyunca, mahkûmun ikileminden tamamen yanlış dersin çıkarıldığını ortaya koydu. Nihayetinde bencillik akılcı bir tutum değildi – oyun bir kereden fazla oynandığı sürece.

Ne gariptir ki, bu muammanın çözümü, oyun daha icat edildiği anda göze çarpmış ve ardından unutulup gitmişti. Flood ve Dresher neredeyse hiç zaman yitirmeden, epey şaşırtıcı bir olguyu keşfettiler. Flood ve Dresher, Armen Alchian ve John Williams adlarındaki iki meslektaşından, düşük miktarda paralarla, oyunu yüz kez oynamalarını istediklerinde, denekler şaşırtıcı bir biçimde işbirliği yapmaya hevesli oldular: Yüz denemenin altmışında her ikisi de işbirliği yaptılar ve yardımlaşmanın meyvelerini topladılar. Her iki oyuncu da oyun boyunca aldıkları notlarda, diğer oyuncuyu iyi davranmaya sevk etmek için, kendilerinin de iyi davranmaya çalıştığını kabul ettiler – ta ki oyunun sonunda, her ikisi de birbirlerini hızla bertaraf etme fırsatını yakalayana dek. Oyle görünüyordu ki, tek bir çift oyuncu tarafından art arda ve süresiz olarak oynandığında, oyuna kötü niyet değil iyi niyet egemen olmuştu.

Alchian- Williams turnuvası unutuldu fakat ne zaman insanlardan bu oyunu oynamaları istense, mantıksal açıdan yanlış taktik olan işbirliğini deneme konusunda kayda değer bir yatkınlık gösterdiler. İşbirliği yapmaya duyulan bu aşırı/yersiz heves, küçümseyici bir biçimde, insanların akılcı olmayışlarına ve çoğunlukla açıklanamayan iyiliksever tutumlarına yoruldu. Bunun üzerine iki oyun kuramcısı “Açıkça görülen o ki, sıradan oyuncuları DD stratejisinin [her iki oyuncunun da döneklik yaptığı durum] mantıken savunulabilir tek strateji olduğunu anlayacak kadar gelişmiş değildirler” diye yazdılar. İnsanlar bunu doğru anlayamayacak kadar kalın kafalıydı.

1970’lerin başlarında bir biyolog, Alchian-Williams oyunundan çıkan dersi yeniden keşfetti. Mühendis-Genetikçi John Maynard Smith, mahkûmun ikilemi kavramını daha önce asla duymamıştı. Fakat Smith, biyolojinin, oyun kuramından, ekonomi kadar faydalanabileceğini fark etti. Smith, tıpkı akılcı bireylerin, oyun kuramının öngördüğü türden stratejileri, herhangi bir koşulda kötünün iyisi olarak benimsemeleri gibi, doğal seçilimin de içgüdüsel olarak benzer stratejileri benimseyen hayvanlar tasarlayabileceğini ileri sürdü. Diğer bir deyişle, bir oyun sırasında Nash dengesini seçme kararına, hem bilinçli ve akılcı çıkarım hem de evrimsel geçmişle varılabilirdi. Salt birey değil, seçilim de karar verebilir. Maynard Smith, [biyoloji alanında] Nash dengesine denk gelen evrimleşmiş içgüdüye “evrimsel sabit strateji” adını verdi: Oyunu oynayan hiçbir hayvan, farklı bir strateji güderek oynayan bir başka hayvandan daha zararlı çıkmayacaktı.

Maynard Smith’in ilk verdiği örnek, hayvanların neden çoğunlukla ölümüne dövüşmedikleri gerçeği üzerine ışık tutmak için bir girişimdi. Smith, oyunu, şahin ile güvercin arasında bir yarışma olarak kurguladı. Mahkûmun ikilemi bağlamında kabaca “dönek”liğe denk gelen şahin, güvercini kolayca alt eder, fakat bir başka şahinle giriştiği kavgada fena biçimde yaralanmıştır. “İşbirliği”yle eşdeğer tutulan güvercin, bir başka güvercinle bir araya geldiğinde bundan fayda sağlar fakat şahine karşı hayatta kalma şansı yoktur. Fakat, oyun tekrar tekrar oynandığında, güvercinin görece uysal nitelikleri daha yararlı hale gelir. Özellikle de Misillemeci stratejisinin –bir Şahinle karşılaştığında kendisi de Şahin kesilen bir güvercin– başarılı bir strateji olduğu görülür.

Maynard Smith’in oyunları, biyoloji alanında olduğundan ekonomistlerce göz ardı edildi. Fakat 1970’lerin sonunda, çok rahatsız edici bir şey olmaya başladı. Bilgisayarlar soğuk, katı ve akılcı beyinlerini, mahkûmun ikilemi oyununu oynamak için kullanmaya başladılar ve tam da aynı şeyi yaparak, budala ve toy insanoğlu gibi, işbirliği yapmak için mantıksızcasına hevesli davranmaya başladılar. Matematik dünyasında tehlike çanları çalmaya başladı. Genç bir siyaset bilimcisi olan Robert Axelrod, 1979 yılında, işbirliğinin mantığını incelemek üzere bir turnuva düzenledi. Axelrod, katılımcıların bir bilgisayar programını çalıştırarak, bilgisayara yüklenmiş diğer her bir programla, bilgisayarın kendisine karşı ve rastgele bir programa karşı oyunu iki yüz defa oynamalarını istedi. Bu büyük yarışmanın sonunda, her program belli bir skor elde edecekti.

On dört katılımcı çeşitli zorluk düzeylerindeki programları çalıştırdı ve şaşırtıcı bir biçimde “iyi niyetli” programların başarılı olduğu görüldü. En iyi niyetli sekiz programın hiçbiri döneklik girişiminde bulunmadı. Dahası, kazanan en iyi niyetli –ve en basit– programdı. Nükleer silahlanma yarışı konusuyla ilgilenen ve mahkûmun ikilemine dair muhtemelen yaşayan herkesten daha fazla bilgi sahibi olan, bir dönemin konser piyanisti, Kanadalı siyaset bilimcisi Anatol Rapoport, Kısasa-kısas denen bir programı çalıştırdı. Bu program gayet basit bir şekilde işbirliği yaparak başlıyor ve ardından da diğer oyuncunun yaptığı son hamlenin aynısını yapıyordu. Tatbikî anlamda Kısasa Kısas, Maynard Smith’in Misillemeci stratejisinin farklı bir isimle ifade edilenidir.

Axelrod bir başka turnuva düzenleyerek, katılımcılardan Kısasa-kısas programını alt etmeye çalışmalarını istedi. Altmış iki program denendi ve buna karşın başarılı olan tek program. Bizzat Kısasa Kısas oldu! Program, diğerlerine karşı yine üstünlük sağladı.

Axelrod’un konuya dair kitabında açıkladığı gibi:

Axelrod’un bir sonraki turnuvası, bir nevi en güçlü olanın hayatta kalma savaşında, stratejileri birbirleriyle yarıştırdı ve bu turnuva, o zamandan beri “’yapay yaşam” olarak bilinen olgunun ilk örneklerinden biri oldu. Evrimin itici gücü olan doğal seçilimin bir simülasyonu, bilgisayarda kolayca yaratılabilir: tıpkı gerçek yaratıkların, gerçek dünyada türeyip, yaşam alanı için rekabete girmeleri gibi, yazılım yaratıklar da bilgisayar ekranında yer kapmak için birbirleriyle rekabet ederler. Axelrod’un uyarlamasında, başarısız stratejiler yavaş yavaş dış kenarlara doğru giderek, meydanı en güçlü programın hâkimiyetine bırakır. Bu bir dizi şaşırtıcı olayı beraberinde getirdi. İlk olarak, kötü niyetli stratejiler, iyi niyetli ve saf stratejilerin pahasına gelişip çoğaldı. Sadece Kısasa Kısas gibi misillemeci stratejiler kötü niyetli stratejilere ayak uydurdu. Fakat sonra, kötü niyetli stratejiler açısından kolay kurbanlar tükenmeye başladı ve bunun yerine sürekli birbirleriyle karşılaşmaya başladılar; kötü niyetli stratejilerin de sayıları giderek azalmaya başladı. Nihayet Kısasa Kısas öne çıkmaya başladı ve bir kez daha, savaş alanının tek hâkimi oldu.

Yarasa Kan Kardeşler

Axelrod, elde ettiği sonuçların biyologların ilgisini çekebileceğini düşündü ve Michigan Üniversitesi’ndeki bir meslektaşı ile temasa geçti. Temas ettiği akademisyen, William Hamilton’dan başkası değildi ve Hamilton derhal bir tesadüfün farkına vardı. On yıldan daha uzun bir süre önce, Harvard’da biyoloji dalında yüksek lisans yapan Robert Trivers adında genç bir öğrenci, Hamilton’a bir makalesini göstermişti. Trivers, hayvanları ve insanları güdüleyen şeyin çoğunlukla çıkar olduğunu varsaymasına karşın sık sık da işbirliği yaptıklarını gözlemlemişti. Trivers, çıkarcı bireylerin işbirliği yapmasının bir nedeninin “karşılıklılık” ilkesi olduğunu ileri sürüyordu: Özetle, sen benim sırtımı kaşı, ben de seninkini. İyiliği yapmanın bedeli, iyiliğin sağladığı faydadan daha az olduğu müddetçe, bir hayvanın yaptığı iyiliğe, ileride her iki tarafa da avantaj sağlayacak biçimde bir başka iyilikle karşılık verilebilirdi. Dolayısıyla özgeci olmak şöyle dursun, sosyal hayvanlar yalnızca bencilce arzulanan iyilik ve yardımlara karşılık veriyor olabilirlerdi. Hamilton tarafından teşvik edilen Trivers, nihayet hayvanlar alemindeki karşılıklılık üzerine tartışma başlatan ve bazı olası örneklerden bahseden bir bilimsel makale yayımladı. Gerçekten de Trivers, tekrarlanan mahkûmun ikilemi kavramını, ileri sürdüğü görüşü sınamak ve iki bireyin etkileşimi ne denli uzun sürerse, işbirliği yapma şanslarının da o denli arttığı yönünde öngörüde bulunmak için bir vasıta olarak tanımlayacak kadar ileri gitti. Esas itibariyle Trivers’ın öngördüğü Kısasa Kısastı.

Şimdi, neredeyse on yıl sonra, Trivers’ın görüşünün sağlam bir geçerliliği olduğuna dair Hamilton’ın elinde matematiksel kanıt vardı. Axelrod ve Hamilton, biyologların dikkatini Kısasa Kısas olgusuna çekmek için “İşbirliğinin Evrimi” başlıklı müşterek bir bilimsel makale yayımladılar. Sonuçta bir ilgi patlaması yaşandı ve hayvanlar arasında gerçek örnekler aranmaya başlandı.

Çok geçmeden bu örnekler bulundu. 1983 yılında, biyolog Gerald Wilkinson, Kosta Rika’dan California’ya biraz ürkütücü bir işbirliği hikayesiyle döndü. Wilkinson, günlerini ağaç kovuklarında yaşayarak, gecelerini ise derilerinde gizlice açtıkları küçük yarıklardan sessizce kanlarını emebilecekleri büyük hayvanlar aramakla geçiren vampir yarasalarını incelemişti. Bu öngörülemez bir yaşamdır; zira yarasalar ya bir hayvan bulamadıklarından ya da avlarının derilerinde açtıkları yaralardan doyurucu miktarda kan emmeleri engellendiğinden, zaman zaman avdan aç dönerler. Yaşlı yarasalar için bu sadece yaklaşık on geceden birinde yaşanır; fakat genç yarasalar üç geceden birinde başarısız olurlar ve bu yüzden üst üste iki gece başarısızlığa uğramaları nadir görülen bir durum değildir. Beslenecek kan bulamadan geçirdiği yalnızca altmış saat gibi bir sürenin ardından, yarasa açlıktan ölme tehlikesiyle karşı karşıya kalır.

Fakat neyse ki, yarasalar çoğunlukla bir öğün sırasında, o andaki ihtiyaçlarından daha fazlasını emebilme şansına sahiptir ve fazladan emilen kan, kusarak geri çıkarma marifetiyle, bir diğer yarasaya bağışlanabilir. Bu cömertçe bir eylemdir ve yarasalar kendilerini bir mahkûmun ikilemi içinde bulurlar: Birbirlerini besleyen yarasalar, beslemeyenlere kıyasla daha karlı çıkarlar; fakat en karlı çıkanları fazla kan emip bunu paylaşmayan, en zararlı çıkanlar ise emdikleri kanı paylaşıp, diğerlerinden kan almayan yarasalardır.

Yarasalar aynı yerlerde konakladıklarından ve uzun bir yaşam sürebildiklerinden –on sekiz yıla kadar- birbirlerini bireyler olarak tanırlar ve tıpkı Axelrod’un bilgisayar programlarında olduğu gibi, oyunu tekrar tekrar oynama fırsatını bulurlar. Yeri gelmişken, vampir yarasaların, tüneyerek konaklayan komşularıyla ortalama olarak çok sıkı akrabalık bağları yoktur ve bundan ötürü cömertliklerinin açıklaması akraba kayırmacılığı değildir. Wilkinson, vampir yarasaların bir anlamda Kısasa Kısas oynadıklarını bulguladı. Geçmişte kan bağışlamış olan bir yarasa, evvelce bağış alan yarasadan kan alacaktır; kan bağışını geri çeviren yarasanın vereceği kan da reddedilecektir. Görünen o ki, her bir yarasa hesap tutma konusunda gayet başarılıdır ve yarasaların düşkün oldukları sosyal tımarlamanın amacı da bu olabilir. Yarasalar, özellikle karın civarındaki bölgeye daha çok özen göstererek birbirlerinin tüylerini tımar ederler. Güzel bir yemeğin ardından karnı şişmiş bir yarasanın, bu şişkinliği karın tüylerini tımar eden diğer bir yarasadan gizlemesi zordur. Dolayısıyla hile yapan bir yarasa çok geçmeden fark edilir. Vampir yarasalar arasında karşılıklı fedakarlığın borusu öter.

Afrika’da yaşayan vervet maymunları da benzer biçimde birbirlerine karşılık verirler. Bir bant kaydından, kavga eden bir maymunun destek çağrısı dinletilen diğer bir maymun, şayet çağrıyı yapan maymun geçmişte yardımda bulunmuşsa, çok daha büyük bir hevesle yardıma koşacaktır. Fakat eğer bu iki maymun yakın akraba ise, ikinci maymunun vereceği tepki, destek çağrısında bulunan maymunun geçmişte yardımda bulunup bulunmadığına pek bağlı değildir. Dolayısıyla, kuramın öngördüğü gibi, Kısasa Kısas akraba olmayan bireyler arasında işbirliği yaratan bir mekanizmadır. Bebekler, annelerinin iyilik ve cömertliğini doğal bir hak olarak görürler ve bunu elde etmek için bir iyi niyet gösterisinde bulunmak durumunda değildirler. Kardeşler kendilerine yapılan her iyi muameleye karşılık verme zorunluluğu hissetmezler. Fakat aralarında akrabalık ilişkisi olmayan bireyler, sosyal borçları konusunda son derece bilinçlidirler.

Kısasa Kısas ilkesinin işlerlik kazanması için gereken temel koşul, istikrarlı ve tekrar eden bir ilişkidir. İki birey arasındaki karşılaşma ne kadar gelişigüzel ve fırsata dayalı ise, Kısasa Kısasın, bir işbirliği tesis etmekte başarı sağlama olasılığı o kadar az olacaktır. Trivers, mercan resiflerinin sıra dışı bir özelliğiyle bu görüşün desteklenebileceğini fark etti: Temizlik istasyonları, Bunlar, resifler üzerinde bulunan belirli yerlerdir ve yırtıcılar dahil, civardaki büyük balıklar buralara gelip daha küçük balıklar ve karidesler tarafından üzerlerindeki parazitlerin “temizleneceğini” bilirler.
Bu şekilde bir temizlik, tropik bir balık olmanın hayati önem taşıyan bir unsurudur. Kırk beşi aşkın balık türü ve en az altı tür karides, mercan resifleri üzerinde temizlik hizmeti sunarlar; bu türlerden bazıları, tek besin kaynağı olarak bu sürece bel bağlarken, çoğu tür de, potansiyel müşterileri tarafından fark edilmelerini sağlayan karakteristik renkler ve faaliyetler sergilerIer. Çoğunlukla açık denizlerden ya da mercanın altında saklandıkları yerlerden çıkıp gelen her türden balık, temizlenmek için bu istasyonlara uğrar ve bazıları temizlenme ihtiyacını belirtmek için özellikle renklerini değiştirirler; büyük balıklar için bu, özellikle değerli bir hizmet gibi görünmektedir. Birçok balık, temizlenmeye, beslenme kadar zaman ayırır ve özelIikle yaralı ya da hasta ise, temizlenmek için günde birkaç kez istasyona uğrar. Eğer bir mercandan temizlikçileri çıkarırsanız, bunun etkisi derhal görülür: Balık sayısı azalır ve parazitler yayıldıkça yara ve enfeksiyon sayısı hızla tırmanır.

Küçük balıklar besin elde eder ve büyük balıklar da temizlenir: karşılıklı fayda sonuç verir. Fakat temizlikçiler çoğunlukla, temizledikleri balığın avladıkları balıklarla aynı biçim ve büyüklüktedirler ve buna rağmen istasyona gelen müşterilerinin ağızlarından içeri girip çıkarak, solungaçlarının arasından yüzerek ve çoğu kez ölüme meydan okuyarak işlerini yaparlar. Ternizlikçiler zarar görmedikleri gibi, müşteriler de yeterince temizlendiklerine inandıklarında yollarına devam etmek üzere olduklarını belirtmek için, dikkatli ve gayet iyi anlaşılan işaretler verirler; temizlikçiler de derhal yaptıkları işi bırakırlar. Temizlenme eylemini yöneten bu içgüdüler öylesine güçlüdürler ki, Trivers’ın bahsettiği bir vakada, bir metre yirmi santimlik uzunluğa erişene dek akvaryumda yetiştirilen ve akvaryuma atılan her balığı havada kapıp vurmaya alışan bir lagos balığı, parazit taşımamasına karşın, denk geldiği ilk temizleyicı balığa, ağzını ve solungaçlarını davetkar biçimde açarak tepki vermiştir.

Buradaki merak konusu, müşterilerin neden “hem karnım doysun, hem de peksimetim bütün kalsın” ilkesine uymadıklarıdır: Temizlik hizmetini kabul edip, ardından temizlikçiyi yiyerek seansı kapatmak! Bu, mahkûmun ikilemindeki dönekliğe eşdeğer olurdu. Ve dönekliğin nadiren görülmesinin nedeni ne ise, bunun önüne geçilmesinin nedeni de tam olarak odur. Bunun cevabı, kaçak çalışan göçmen temizlikçisinin işine son verip, ertesi hafta yeni bir temizlikçiyle anlaşmaktansa, neden temizlik bedelini ödeme külfetine katlandığı sorusuna, ahlaksız bir New Yorklunun muhtemelen vereceği cevapla aşağı yukarı aynıdır: Çünkü iyi temizlikçi bulmak kolay değildir. Mercanlardaki temizlik istasyonlarının müşterileri olan balıklar, kendilerinden sonraki müşterilere karşı bir sorumluluk hissi taşımalarından ötürü değil, iyi bir temizlikçinin, kendileri için halihazırda bir yemekten çok gelecekte bir temizlikçi olarak daha büyük değer taşımasından ötürü, temizlikçi balıklara kıymazlar. Bunun yegane sebebi, aynı temizlikçinin, aynı resifin aynı noktasında, her gün, yıllar boyunca bulunabilmesidir. İlişkinin devamlılığı ve süresi denklem için hayati önem taşır. Tek seferlik karşılaşmalar/ilişkiler, dönekliğe çanak tutar; sık sık tekrar edenler ise işbirliğini teşvik eder. Açık denizlerin göçebe yaşamı içerisinde temizlik istasyonları bulunmaz.

Axelrod’un incelediği diğer bir örnek, Birinci Dünya Savaşı’nın Batı Cephesi idi. Taraflar bir türlü yenişemediğinden, savaşı aynı toprak parçası uğruna uzun bir çatışmaya dönüştü; öyle ki, iki birlik arasında tekrar tekrar yinelenen çarpışmalar yaşandı. Bu tekrarlar, mahkûmun ikilemi oyunundaki tekrarlar gibi, akılcı taktiğin düşmanlıktan işbirliğine dönüşmesine yol açtı ve gerçekten de Batı Cephesi’nde, bir süreden beri birbirleriyle çarpışan Müttefik ve Alman birlikleri arasındaki gayri resmi ateşkes antlaşmaları “salgın hastalık” gibi yayıldı. Koşullar üzerinde anlaşmak, kazara ihlaller için af dilemek ve görece barışı temin etmek üzere ayrıntılı iletişim sistemleri geliştirildi – tüm antlaşmalar her iki tarafın da üst düzey komuta kademesinin bilgisi dışında gerçekleşti. Ateşkes antlaşmaları basit bir misilleme anlayışıyla kontrol altına alındı. Karşı tarafın dönekliğini cezalandırmak için baskınlar ve ağır silahlarla yaylım ateşi devreye sokuldu ve tıpkı kan davalarının kontrolden çıkması gibi, intikama dayalı bu önlemler de zaman zaman tırmanarak kontrolden çıktı. Dolayısıyla bu durum, Kısasa kısas stratejisiyle büyük bir benzerlik arz ediyordu: İşbirliği yaratarak, dönekliğe, döneklikle karşılık veriyordu. Ateşkes antlaşmaları su yüzüne çıktığında, her iki tarafın da generallerinin uygulamaya koyduğu basit ve etkili “çare”, birlikleri sık sık nakletmek oldu; böyIece hiçbir birlik, işbirliğine dayalı bir ilişki kuracak kadar uzun müddet karşılıklı cephelerde yer almıyordu.

Fakat Birinci Dünya Savaşı bahsi, Kısasa kısas’ın karanlık bir yanı olduğunu bize hatırlatır. Eğer Kısasa kısas oyuncuları karşı karşıya gelip, doğru adımlarla oyuna başlarlarsa, süresiz bir işbirliği içine girerler. Fakat şayet aralarından biri kazara ya da düşünmeden döneklik yaparsa, o zaman bir dizi karşıIıklı suçlama kaçınılmaz hale gelir. Ne de olsa, Sicilya, on altıncı yüzyıldaki İskoç sınırları, antik Yunan ve günümüzün Amazon yağmur ormanları gibi, geçmişte ve günümüzde insanların fitneye dayalı kan davası ve intikam bağımlısı haline geldikleri yerlerde “kısasa kısas cinayeti” deyişinin anlamı budur. Kısasa kısas, her derde deva olan evrensel bir çare değildir.

Fakat insanlar adına çıkarılacak ders, karşılıklı fedakarlık ilkesinin toplumda sık sık kullanılmasının, doğamızın kaçınılmaz bir unsuru olabileceğidir: bir içgüdü. “Yapılan iyilik karşılıksız kalmaz” sonucuna nasıl vardığımızı gerekçelendirmeye ya da aksini düşünmemize rağmen bunun bize öğretilmesine ihtiyaç duymayız. Bu, bizler olgunlaştıkça içimizde gelişen bir kavram, duruma göre öğretilerek veya doğal biçimde öğrenilerek gelişen, kökü kazınmaz bir eğilimdir. Peki neden? Çünkü doğal seçilim, karşılıklılık olgusunu, sosyal yaşamdan daha fazla faydalanabilmemiz için seçmiştir.
——————————————————
(Kaynak: Matt Ridley, Erdemin Kökenleri (The Origins of Virtue – Chapter Three – The Prisoner’s Dilemma)